Prove That Root 2 Is An Irrational Number
Taking squares on both sides we get. 8 1 1a rational irrational real numbers scimathmn Square Root Rational Number.

Prove That Square Root Of 2 Is Irrational Youtube
3 2 abwhere a and b are integers and b is not equal to zero.

Prove that root 2 is an irrational number. Here we are going to see how to prove the given number is irrational. 5 pq.
So it can be expressed in the form pq where pq are co-prime integers and q0. 2 a 2 b 2. Well the assumption should give us a hint where to start.
2 is an irrational number. It cannot be given as the ratio of two integers. On squaring both the sides we get.
Therefore p is an even number that divides q. Let us assume that 5 is a rational number. To prove that root 2 is an irrational number.
B 2 2c 2. You may wonder what our next step be. Now apply square on both sides.
Let a 2c. To prove that the square root of 2 is irrational is to first assume that its negation is true. How do you prove 3 Root 2 is irrational.
I assume that we know that square root of two is irrational this by contradiction as many proofs on irrationality we assume it is rational that means that 2sqrt 2 a and a is rational that means that a-2 is rational and thus sqrt 2 is rational which is not thus contradiction thus it is irrational. If it were rational it would be expressible as a fraction ab in lowest terms where a and b are integers at least one. So it can be expressed in the form pq where p q are co-prime integers and q0.
The square root of 2 is represented as 2. Let 2 be a rational number. How to Prove the Given Number is Irrational.
26 is an irrational number 2 is a rational number 6 is an irrational number Sum of rational number and irrational number is an irrational number. Here are a number of highest rated Square Root Rational Number pictures upon internet. Any number that has a non-terminating and non-repeating decimal expansion is always an irrational number.
Thus A must be true since there are no contradictions in mathematics. 3 rows Here is where mathematical proof comes in. A different approach is using polynomials and the rational root theorem.
Medium Open in App Solution Verified by Toppr Let us assume on the contrary that 2 is a rational number. Answer 1 of 4. The actual value of 2 is undetermined.
But this contradicts the fact that 2 is irrational. The decimal expansion of 2 is infinite because it is non-terminating and non-repeating. If p divides a 2 then p divides a.
By the Pythagorean Theorem the length of the diagonal equals the square root of 2. Then there exist positive integers aand. Let us assume that 2 is a rational number with p and q as co-prime integers and q 0 2 pq On squaring both sides we get 2q 2 p 2 p 2 is an even number that divides q 2.
Therefore we assume that the opposite is true that is the square root of 2 is rational. So 2 is an irrational number. To prove that 2 is an irrational number we will use the contradiction method.
Therefore 2 3b ab is rational as a b and 3 are integers. Our supposition 2 5 is a rational number is wrong. Prove that 2 is an irrational number.
Here 2 3 is irrational. Therefore there exists no rational number r such that r 2 3. Prove that 2 is an irrational number.
By the rational root theorem possible roots are xpm 1 or xpm2 Next check that f-2 f-1 f1 f2 not 0. Let as assume that 2 3 is a rational number. If possible let us assume 2 5 is a rational number.
So the square root of 2 is irrational. So assumption was incorrect. Proof that root 2 is an irrational number.
We want to show that A is true so we assume its not and come to contradiction. So 2 can be expressed in pq form where p q is not equal co primes where q is not equal to 0. A 2 divides 2 That is 2a 2 Then a also divides 2.
2 5 is an irrational number. Prove that root 5 is irrational number. 2b 2 a 2.
The proof that 2 is indeed irrational is. How do you prove 3 is irrational. Irrationality of the square root of 2.
The following proof is a classic example of a proof by contradiction. Let p be a prime number and a be a positive integer. A classic proof by contradiction from mathematics is the proof that the square root of 2 is irrational.
Since sqrt32 is a root of fxx3-2 it is enough to show that if fx has no rational roots then sqrt32 is irrational. Then there exists co - prime positive integers p and q such that. From the contradiction approach also known as the Euclidian approach let us assume that root 2 is a rational number.
We need to prove that 5 is irrational. Let us assume that 2 is a rational number. This contradicts the fact that 3 is irrational.
By applying the value here we get. Sal proves that the square root of 2 is an irrational number ie. 2 5 q p where p q z q 0 2 q p 5 q 2 q p 5 5 is a rational number q 2 q p is a rational number But 5 is not a rational number.
Then it may be in the form ab. Prove that 2 is an irrational number. A real number that is not rational is called an irrational number.
2b 2 a 2. 2b 2 4c 2. 2b 2 2c 2.
The Square Root Of Two Making Your Own Sense
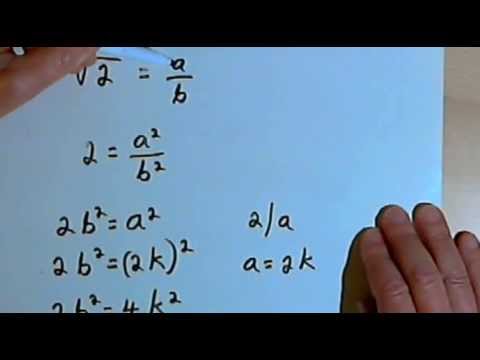
Proof That The Square Root Of 2 Is Irrational 127 4 21 Youtube
The Square Root Of Two Making Your Own Sense

Solved Proof That Root 2 Is Irrational Brainly In

Prove That Under Root 2 Is Irrational Number Youtube

Proof 2 Is Irrational Hindi Youtube
Prove That Root 2 3 Is An Irrational Number Studyrankersonline

Understanding The Proof Of Sqrt 2 Is Irrational By Contradiction Mathematics Stack Exchange

Theorem 1 4 Root 2 Is Irrational Chapter 1 Real Number Class 10th In Hindi Youtube

Prove That Root 2 Is Irrational Number Is Root 2 An Irrational
The Square Root Of Two Making Your Own Sense

How To Adapt Proof By Contradiction Showing That A Sqrt 2 Is Irrational For Sqrt 20 Mathematics Stack Exchange
Why Does 2 7 An Irrational Number Prove That 2 7 Is Irrational Quora

Irrationality Of The Square Root Of 2
Posting Komentar untuk "Prove That Root 2 Is An Irrational Number"